Single-Member Districts: Divide and Conquer

A small, square town of 225 voters wants to elect a 15-member council to govern its public affairs. Most of them (72 percent) are affiliated with the Purple Party, and 28 percent are in the Aqua Party.

How should it choose its members?

It seems natural that the Purple Party should end up with 11 seats (73 percent) and the Aqua Party should get 4 seats (27 percent). In this case, more than 96 percent of voters would be represented by someone who they support.

Instead, the town arranged to divide itself into 15 districts. Each district separately votes for its own representatives. It was left to politicians to decide how the districts are drawn on the map.

After deciding this, the townsfolk forgot about it, because it seemed like a complicated detail. But they have made a fundamental logical error: they are allowing only a majority of voters to obtain representation, and a majority of those representatives can pass laws. A majority decision means that more people support the decision than oppose it. But when decisions are made by a majority of a majority, a small fraction of voters can overrule everyone else. Furthermore, an even smaller group of people can control which fraction of voters has this power. Under this arrangement, voters have a political role similar to that of the Queen of England.

In our square town, it turns out that the Aqua Party controls the district-drawing committee. After feeding party registration data, precinct data from previous elections, and other such information into a sophisticated computer program, they produce the following map, a horizontal 3x5 grid:

With these district lines, Aqua voters outnumber Purple voters in a majority of districts. After the election, the Purple voters in those districts - 25 percent of the total - are left disenfranchised; they are represented by someone who they explicitly oppose. Representatives of 28 percent of the voters have the power to dominate the council and pass laws at their whim. The 7 other representatives can only voice their objections.

It shouldn't be this way, right? That's what the Purple politicians think. So by some means they manage to take control of the district-drawing committee and obtain vengeance. Their computer recommends that they turn the districts sideways.

After the election, the Purple Party has taken all 15 seats, and the Aquas have no voice at all on the town council.

You can be assured that the district-drawing committee could obtain just about any result between these two extremes by drawing different boundary lines. They have even more power if there are more than two political parties, and if elections are decided by a "most votes wins" rule rather than majority rule.

Invariably, the committee will do everything it can to preserve the positions of the politicians in power. The result is that, instead of a representative government based on diverse, competitive elections, the town is divided into small fiefdoms where politicians exercise absolute power, insulated from threats from their peers - and, to a large extent, from voters. It could be said that council members have more to fear from the district-drawing committee than voters or anyone else.

While California is not a square, the other parts of this story are disturbingly realistic. In the November 2002 election, representatives supported by 24 percent of voters gained the power to pass laws in the legislature. Voters live in contorted districts like

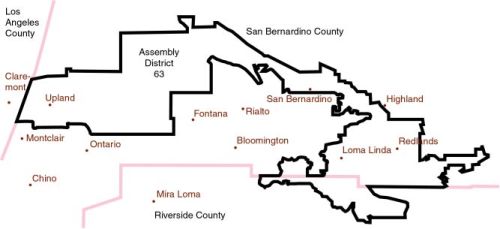
Many incumbent legislators donated tens of thousands of dollars to support the political consulting firms that create such fine art. In that election, every single politician running for re-election to a state or federal office was successful.

It doesn't have to be this way. There are many ways to arrange elections so that just about everyone has a voice on a town council or in a state legislature, chosen from a diverse and competitive pool. Californians for Electoral Reform is a statewide group that promotes some of them. Please read our introduction to learn more about these.